Towards Accurate Multi-person Pose Estimation in the Wild (CVPR 2017)

2020-03-18 · 5 min read

2017 Google Pose CVPR

Goal
解析文中令人费解的霍夫投票公式

文章链接: arXiv
作者信息:

George Papandreou, Tyler Zhu, Nori Kanazawa, Alexander Toshev, Jonathan Tompson, Chris Bregler, Kevin Murphy
Google, Inc.

Overview

基于深度学习的人体姿态/关键点检测常用的方法有以下几种:

基于回归的方法: 直接通过网络回归出图像中人体关键点的坐标, 这种方法在早期(2014年左右)有使用, 但由于回归任务很难训练, 现在(2020年)几乎看不到了
基于分类的方法: 将人体关键点检测看作类似分割的任务, 通常在关键点处放置高斯核作为监督信号, 让网络输出热图(heatmap), 以表示关键点可能的位置及其概率, 再通过一些后处理的手段从热图得到关键点坐标. 这种方法中, 关键点位置实际上是一片区域, 而不仅仅是一个点, 网络容易学习. 不足之处就是由于最终热图的尺寸降采样很严重, 由量化误差导致的性能损失较多
分类与回归相结合的方法: 据我所知, 本文应该是最早结合分类与回归的方法. 这种方法为每个位置预测当前位置到关键点的偏移量, 然后基于霍夫投票的思想, 把关键点附近的各个位置的偏移量的预测加和起来, 可以得到更准确的关键点位置. 但是由于本文没有开源代码, 而且霍夫投票的这个公式写的极难理解, 导致很多人只能通过文中图2去猜测实际的做法. 本篇博客旨在详细解析该论文的公式(1)

Heatmap and Offset Prediction with CNN

Network Output

$K$ 为关键点的数量, 网络的输出的channel数为 $3K$ , 即每个关键点有3层输出. 其中1层是heatmap, 本文中是一个二值的mask. 其余两层是offset, 其值表示该位置在 $x$ 和 $y$ 方向与关键点的距离.

Heatmap

Heatmap应该很好理解, 本文中使用的是二值的mask, 关键点周围圆形区域值为1, 其他位置值为0. Heatmap表示了关键点位置的粗略估计, 即关键点周围的一片圆形区域, 如上图中红色区域.

Offset

已经通过heatmap的学习得到了关键点的粗略位置, 但是图中红色区域内都有可能是关键点所在位置, 具体在哪一个位置呢? 可以通过霍夫投票的方式, 综合考量多个位置处对于关键点所在位置的预测, 得到一个细化的预测.
Offset的ground-truth如上图的最右子图. Offset有两个channels, 这里画出的应该是两个channel的值的平方和的根, 也即欧式距离. 距离关键点越远, 值/距离越大, 但到了heatmap圆形区域外的部分忽略.

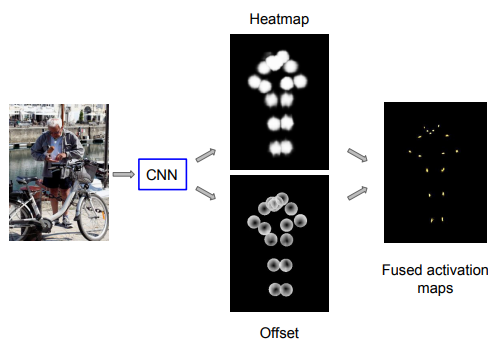
f_{k}\left(x_{i}\right)=\sum_{j} \frac{1}{\pi R^{2}} G\left(x_{j}+F_{k}\left(x_{j}\right)-x_{i}\right) h_{k}\left(x_{j}\right)

$f_{k}\left(x_{i}\right)$ 在文中被称为highly localized activation maps, 对应下图最右的fused activation maps. $x_{j}+F_{k}\left(x_{j}\right)$ 表示的是位置 $x_{j}$ 对于关键点所在位置的预测, 把这些预测加和起来就实现了霍夫投票, 得到一个更为精细的关键点位置预测. 这里最令人费解的是 $G(\cdot)$ -- the bilinear interpolation kernel, 文中完全没有对此的详细说明. 我猜测 $G(\cdot)$ 应该是一个输入2D向量, 输出一个标量的函数. 2D向量是 $x_{j}+F_{k}$ 与 $x_{i}$ 的offset, offset越大, 输出值越接近0, 那么 $f_{k}\left(x_{i}\right)$ 值越小, 表示 $x_{i}$ 位置不太可能是关键点位置.

Comments

这篇文章提出的霍夫投票的思路得到refined关键点位置其实很有意思. 只通过heatmap, 由于降采样导致的量化误差很大, 会影响最终关键点位置的精度. 如果在全图上用回归的方法找关键点位置, 虽然理论上可以做到无限精度, 但是实际网络很难训练好. 本文通过heatmap的方式找到关键点所在的大概位置, 然后在一个较小的区域内用回归的方法去找更精细的关键点位置, 结合了以上两种方式的优点. 后续也有一些工作采取了类似的做法, 比如PIFPAF.