畸变参数造成的「鬼影」
一个由于相机畸变参数导致的奇妙现象
Intro
假设现有多视角相机3个, 空间某点 在第1,2个相机的投影分别为 和 , 不在第3个相机的视野范围内, 故在相机3的像上应该没有对应点.
然而, 当我们按照相机参数把 投影到第3个相机时, 奇妙的事情发生了, 由投影到图像得到的坐标居然在图像的范围内!
那么, 问题出在哪里?
A Demo
以下是我们项目中实际使用的相机的内参.图像尺寸为 .
f=1061
cx=960
cy=540
畸变参数为:
k = [-0.33, 0.12, -0.022]
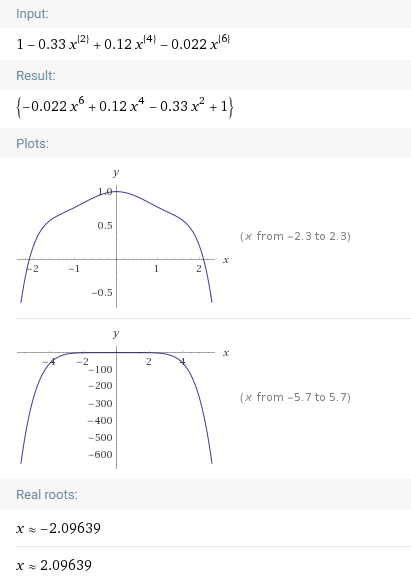
那么, 实际的畸变系数[1]为:
由于相机镜头畸变, 导致坐标从相机坐标系通过内参转换到uv坐标系时, 要乘以系数.
若仅考虑轴方向, 则
为简化问题, 我们仅考虑 的情况, 将式(1)代入式(2), 得到
以上, 得到了uv坐标系与相机坐标系的坐标换算关系. 已知图像宽度1920, 也就是.
式(3)的函数图像如下图
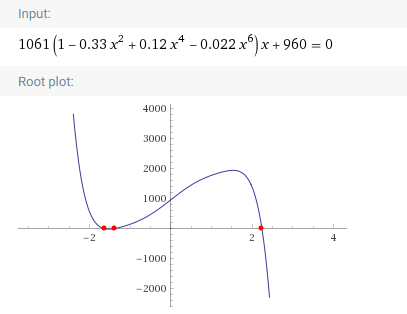
当 时, 3个实根为 ;
当 时, 3个实根为 .
从图和根之间大小关系可知, 当 时, 的范围大致为 (其中有些小区间不严格满足).
再根据 焦距 和 可知, 当 时, 点才在实际图像范围内. 但由于畸变参数的影响, 当 都能使得到的像点在图像成像/视野范围内.
Summary
以上的例子已经很具体的说明了「鬼影」的成因.
回到问题的本质, 其实还是由于相机畸变模型本身存在的缺陷导致的. 径向畸变的第二和三个参数分别是距离的4次方和6次方的系数, 当距离增大时, 这些项急剧地变化, 导致算出来地相机畸变补偿系数严重偏离真实的值. 相机的畸变模型应用范围是局限相机成像范围内的, 当脱离了这个前提, 事情就开始变得丑陋了.
畸变对于投影相机模型来说, 是一个外挂的存在, 破坏了原本流畅美丽的投影关系变换. 对于计算基础矩阵以及进行 Triangulation 等任务也非常头疼, 事先把图像的畸变校正掉, 会省去自己很多的麻烦.
Appendix