相机参数与基础矩阵笔记

Highligh:

• 详解相机位姿和外参的关系
• 详解基础矩阵(Fundamental Matrix)的计算

位姿(Pose)与相机外参

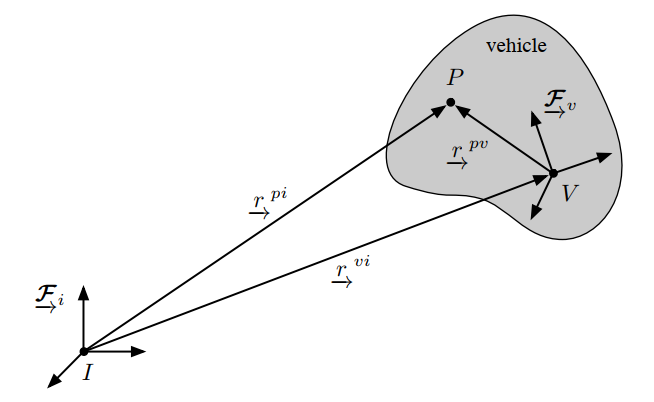
图 1. 物体的位姿(pose)示意图, 图来自^[1]

如图1所示, 图中各量满足

$\mathbf{r}_{i}^{p i}=\mathbf{C}_{i v} \mathbf{r}_{v}^{p v}+\mathbf{r}_{i}^{v i} \tag{1}$

其中$I$是惯性系, 也即全局坐标系. $V$是体坐标系, 即物体自身定义的坐标系. $P$是空间中一点.
$\left\{\mathbf{r}_{i}^{v i}, \mathbf{C}_{i v}\right\}$ 定义为物体$V$在全局坐标系$I$中的位姿.
可以看出, 位姿包括平移和旋转两部分, 平移分量$\mathbf{r}_{i}^{v i}$表示$V$在$I$坐标系中的位置表达, 旋转分量$\mathbf{C}_{i v}$表示$V$到$I$的旋转关系.
显见, 上式表达的是将坐标从$V$系转换到$I$系.

而在常见的相机参数表示中, 相机外参${R, t}$表示相机的"位姿", 但是具体含义又与前述机器人学中的含义不尽相同, 加之旋转本就比较难以直观理解, 经常容易犯错.
投影相机(§ 6.2 in ^[2] or § 6.4.1 in ^[1:1])外参的作用是将空间中的点$x$的坐标$x_{I}$从全局坐标系$I$ 转换到相机坐标系, 这里记作$C$吧, 与前文中$V$其实是一样的. 转换关系为

$x_{C} = R\cdot x_{I} + t \tag{2}$

可见, 该式表达的是将坐标从全局坐标系$I$转换到相机的自身坐标系$C$.
至此, 位姿和外参的关系就很清晰了. 他们表示的变换方向是相反的.

对于实际问题, 我们常会遇到五花八门的相机参数提供方式, 有按标准提供外参的, 有提供相机位姿的, 还有提供经过奇怪变换后的平移旋转参数的. 牢记以上两个公式, 然后进行一些推导变换, 即可正确解析.

典型题1: 已知相机外参 $\{R, t\}$, 求相机位姿.
公式$(2)$两边同乘 $R^{\top}$ 可得 $R^{\top} \cdot x_{C} = x_{I} + R^{\top} \cdot t$ , 即 $x_{I} = R^{\top} \cdot x_{C} + (-R^{\top} \cdot t)$.
所以相机位姿为 $\{(-R^{\top}t), R^{\top}\}$.

典型题2: 已知相机位姿 $\{r, C\}$, 求相机外参.
可知 $x_{I} = C \cdot x_{C} + r$, 两边同乘 $C^{\top}$ 可得 $x_{C} = C^{\top} \cdot x_{I} + (-C^{\top} \cdot r)$.
即相机外参为 $\{C^{\top}, -C^{\top}r \}$.
且 $\left[\begin{array}{ll} \mathbf{C} & \mathbf{r} \\ \mathbf{0}^{T} & 1 \end{array}\right]^{-1} = \left[\begin{array}{ll} \mathbf{C^{\top}} & \mathbf{-C^{\top}r} \\ \mathbf{0}^{T} & 1 \end{array}\right]$.

(注意: 本文中位姿和外参中旋转和平移分量的位置不同.)

基础矩阵(Fundamental Matrix)

(§ 9.2.2 in ^[2:1])提供了一个示例用于在已知两个相机参数的情况下, 计算其之间基础矩阵.

$\mathrm{F}=\mathrm{K}^{\prime-\top}[\mathbf{t}]_{\times} \mathrm{RK}^{-1} \tag{3}$

但相机1的参数被设定为了 $\mathrm{P}=\mathrm{K}[\mathrm{I} | \mathbf{0}]$, 导致在实际使用时不能直接套用该公式.

实际用例:
已知两相机参数分别为$\mathrm{P_{1}}=\mathrm{K_{1}}[\mathrm{R_{1}} | \mathbf{t_{1}}]$ 和 $\mathrm{P_{2}}=\mathrm{K_{2}}[\mathrm{R_{2}} | \mathbf{t_{2}}]$.
为了能代入公式(3)需要引入一个变换将相机1的外参变为$[\mathrm{I} | \mathbf{0}]$, aka 对全局参考系进行旋转平移, 使得相机1外参变为$[\mathrm{I} | \mathbf{0}]$.

已知 $x_{I^{\prime}} = R_{1}\cdot x_{I} + t_{1} = x_{C}$, 其中$I^{\prime}$是变换后的坐标系, 坐标系$I$在$I^{\prime}$中的位姿为$\{t_{1}, R_{1}\}$ 可见该变换恰可以让相机1的外参变为$[\mathrm{I} | \mathbf{0}]$.

将相机2也变换到 $I^{\prime}$坐标系中, $x_{I^{\prime}} = R_{1}\cdot x_{I} + t_{1}$,
又有 $x_{I} = R^{\top} \cdot x_{C} + (-R^{\top} \cdot t)$,
可得 $x_{I^{\prime}} = R_{1}\cdot (R_{2}^{\top}\cdot x_{C} + (-R_{2}^{\top} \cdot t_{2})) + t_{1}$,
即 $x_{C} = R_{2}R_{1}^{\top}\cdot x_{I^{\prime}} + (t_{2} - R_{2}R_{1}^{\top}t_{1})$

最终相机2的外参变换为 $[(\mathrm{R_{2}R_{1}^{\top}}) | (\mathrm{t_{2}-R_{2}R_{1}^{\top}t_{1}})]$, 且相机1外参为$[\mathrm{I} | \mathbf{0}]$.

def get_fundmat(cam1, cam2):
    """
    Transform cams that cam1's R is identity mat and t is zero vector
    $F = \mathrm{K}^{\prime-\top}[\mathrm{t}]_{\times \mathrm{RK}^{-1}}$
    1′=Fx
    :param cam1:
    :param cam2:
    :return:
    """
    K1 = cam1['K']
    K2 = cam2['K']
    R1 = cam1['R']
    R2 = cam2['R']
    t1 = cam1['t']
    t2 = cam2['t']
    R22 = R2 @ R1.T
    t22 = (t2 - R22@t1).reshape(-1)

    t_mat = np.zeros((3, 3))  # cross product matrix
    t_mat[0, 1] = -t22[2]
    t_mat[0, 2] = t22[1]
    t_mat[1, 2] = -t22[0]
    t_mat = -t_mat.T + t_mat

    fundmat = np.linalg.inv(K2).T @ t_mat @ R22 @ np.linalg.inv(K1)
    return fundmat

参考资料